Topology optimization is one promising approach to enhance the performance of a device and
has been applied to produce many devices in engineering.
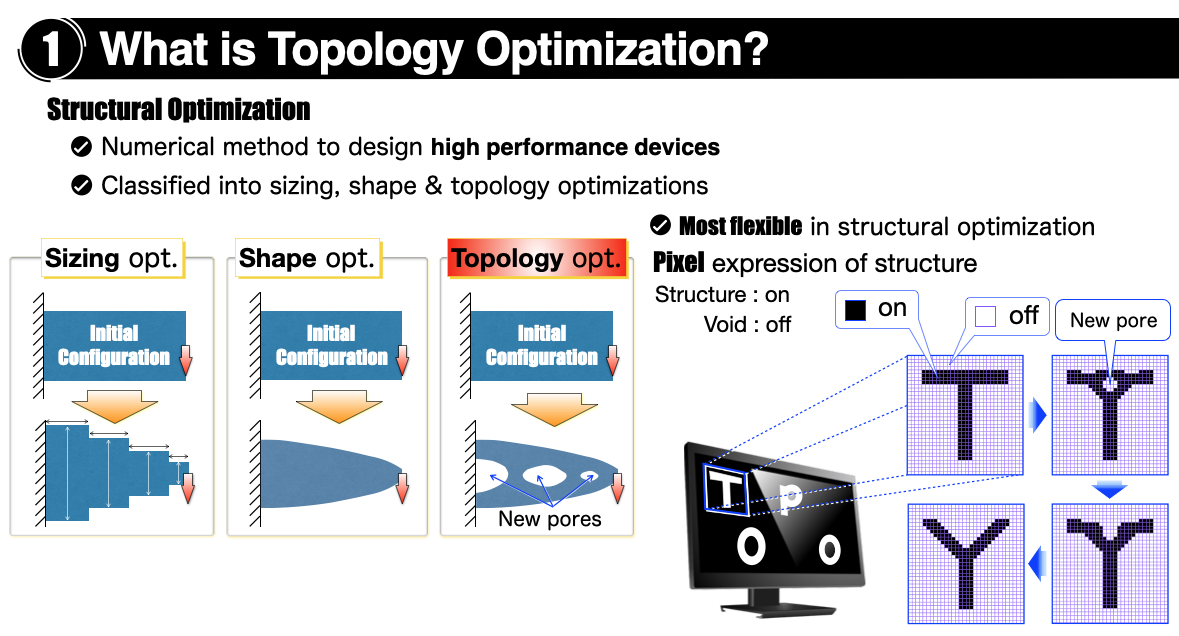
The structural topology can be changed during topology optimization to improve performance;
the highest degree of design freedom in structural optimization can provide the highest performance.
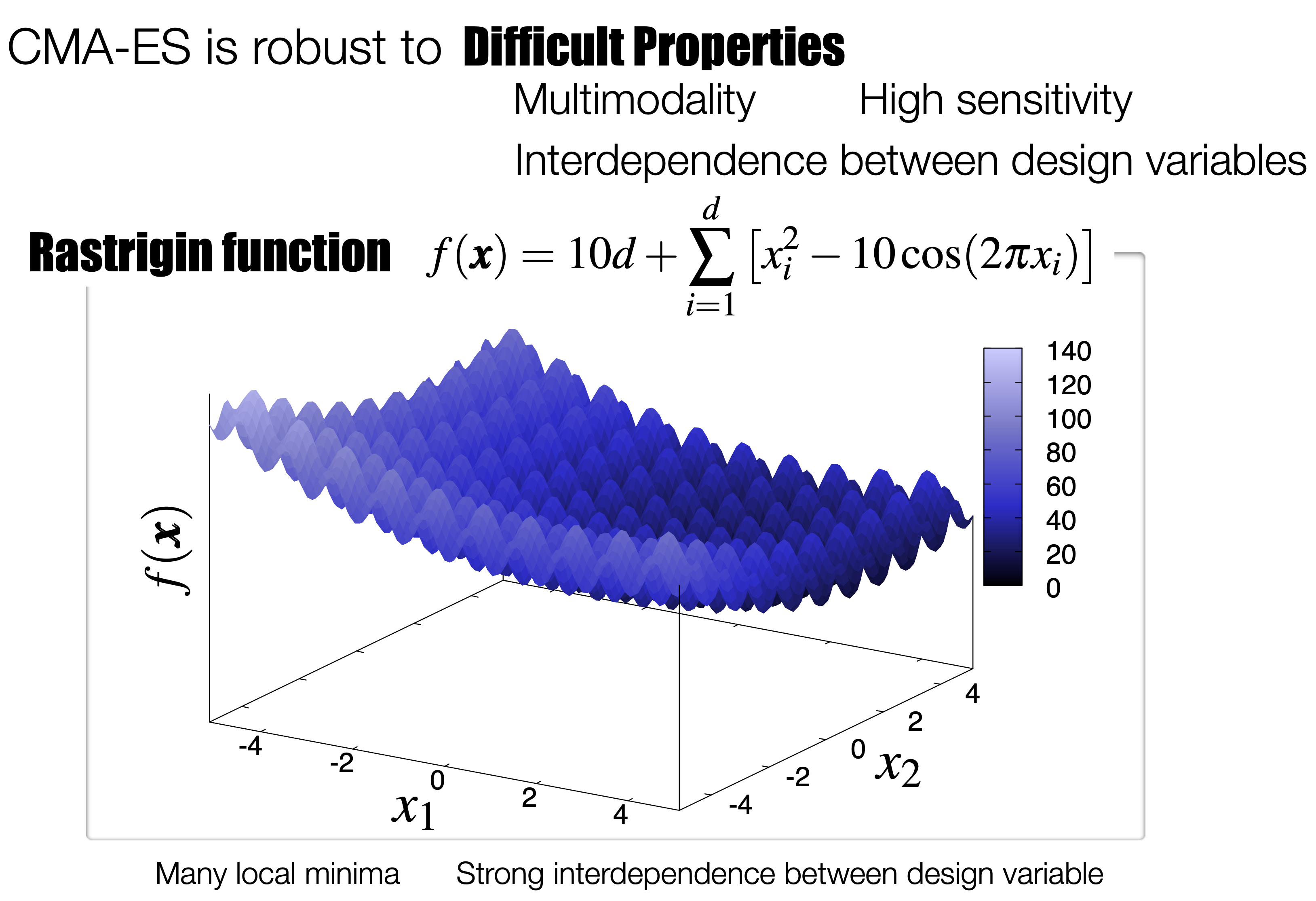
However, apart from the freedom of the structure, topology optimization involves various difficulties for each problem. For example, there are various problems such as multi-modal nature, where many local optimal solutions with insuficient performance exist, the curse of dimensionality, where the optimal solution cannot be obtained because the number of possible structures increases exponentially in a problem with a large number of design variables, and dependency between design variables, where relative changes in many design variables affect the objective function.
Our mission is to develop a topology optimization method that can solve these problems simultaneously.
However, apart from the freedom of the structure, topology optimization involves various difficulties for each problem. For example, there are various problems such as multi-modal nature, where many local optimal solutions with insuficient performance exist, the curse of dimensionality, where the optimal solution cannot be obtained because the number of possible structures increases exponentially in a problem with a large number of design variables, and dependency between design variables, where relative changes in many design variables affect the objective function.
Our mission is to develop a topology optimization method that can solve these problems simultaneously.

Optimization problems range from simple convex functions to multimodal functions with many local optimal solutions.
In topology optimization, the nature of the optimization problem varies greatly depending on
its objective function to be minimized, constraints, and physical field(s) of interest.
Topology optimization problems related to wave manipulations, such as electromagnetic and sound waves, which have recently attracted much attention due to the emergence of metamaterials and photonic/phononic crystals, are generally difficult structural design problems due to the strong multimodality and dependence among design variables caused by the scattering and interference inherent to waves. This research aims to develop topology optimization methods capable of solving optimization problems that remain unresolved due to these challenging properties.
Topology optimization problems related to wave manipulations, such as electromagnetic and sound waves, which have recently attracted much attention due to the emergence of metamaterials and photonic/phononic crystals, are generally difficult structural design problems due to the strong multimodality and dependence among design variables caused by the scattering and interference inherent to waves. This research aims to develop topology optimization methods capable of solving optimization problems that remain unresolved due to these challenging properties.
Because topology optimization is an ill-posed problem, various structural modeling approaches have been proposed.
The high degree of design freedom of topology optimization can create spatially infinitely small structures,
requiring structural modeling and constraints to control them.
In these topology optimizations, the resulting optimal configurations may differ depending on the structural modeling method. The ease of fabrication also depends on the clarity around the contours of the optimized structure.
In addition, by making structural modeling and spatial discretization (finite element size) independent of each other, high computational accuracy and low dimensionality can be achieved, which in turn leads to faster calculations.
In these topology optimizations, the resulting optimal configurations may differ depending on the structural modeling method. The ease of fabrication also depends on the clarity around the contours of the optimized structure.
In addition, by making structural modeling and spatial discretization (finite element size) independent of each other, high computational accuracy and low dimensionality can be achieved, which in turn leads to faster calculations.

